跳转至

Chapter9 Graph Algorithms

Definitions

G(V, E)：

  • G：图
  • V = V(G)：有限的非空顶点集合
  • E = E(G)：有限的边集合

Undirected graph：无向图，\((v_i,v_j)=(v_j,v_i)\)，是同一条边

Directed graph (digraph)：有向图，image-20231113142616856

  • Self loop is illegal. 环是不合法的
  • 不考虑Multigraph（重复的边）

Complete graph：具有最大边个数（不考虑multigraph）的图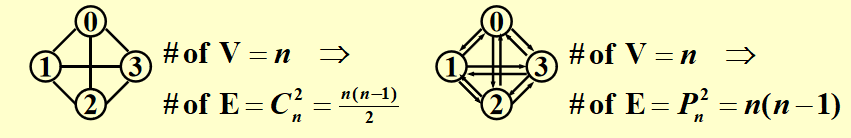image-20231113142851270

adjacent： - 无向图：\(v_i\) and \(v_j\) are adjacent / \((v_i,v_j)\) is incident on \(v_i\) and \(v_j\) 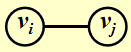image-20231113143319760 - 有向图：\(v_i\) is adjacent to \(v_j\) / \(v_j\) is adjacent from \(v_i\) / \(<v_i,v_j>\) is incident on \(v_i\) and \(v_j\)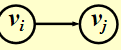 image-20231113143519400

Subgraph G' \(/subset\) G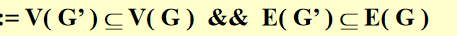：image-20231113143717957

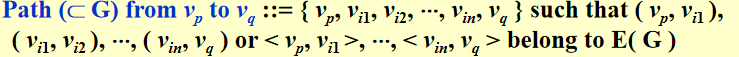
Path(\(/subset\) G) from \(v_p\) to \(v_q\)：路径 image-20231113143946934

Length of a path：路径的长度就是路上的边的数量

Simple path：每个包含的角（不包括起点终点）都只经历了一次的路径

Cycle：是一个simple path 且 起点等于终点

connected：

  • 无向图：
    • 角的联通 - 有路径
    • 图的联通 - 任意两个角联通
  • 有向图：
    • 强联通
    • 弱联通

(Connected) Component of an undirected G：最大联通子图

tree：无环连通图

DAG：有向无环图

Degree(v)：image-20231113144757445

  • 握手法则：image-20231113144925522

Representation of Graphs

Adjacency Matrix

image-20231113145158893

对时间和空间复杂度浪费较多

Adjacency Lists

把每一行用链表替代 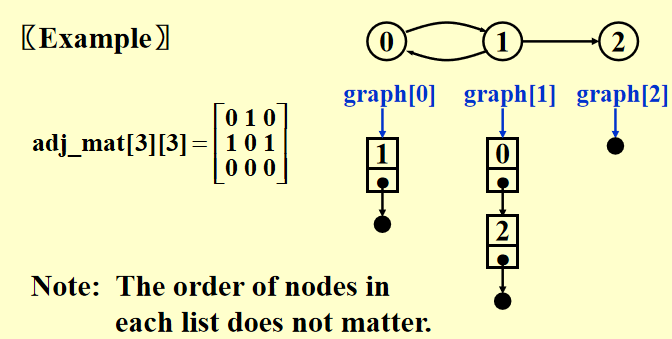image-20231113145620909

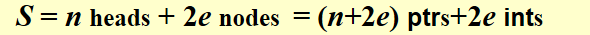
image-20231113145736130

无向图的degree和有向图的out-degree都可以通过graph[i]的节点数获得

如果是处理有向图的in-degree，那么应该

  • 方法1：把每一列用链表处理，得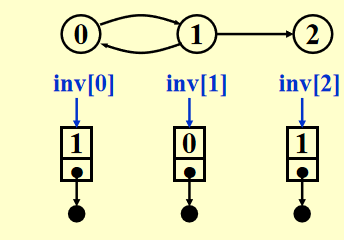：image-20231113150041339 （Inverse Adjacency Lists）
  • 方法2：构建Multi-list

Adjacency Multi-lists

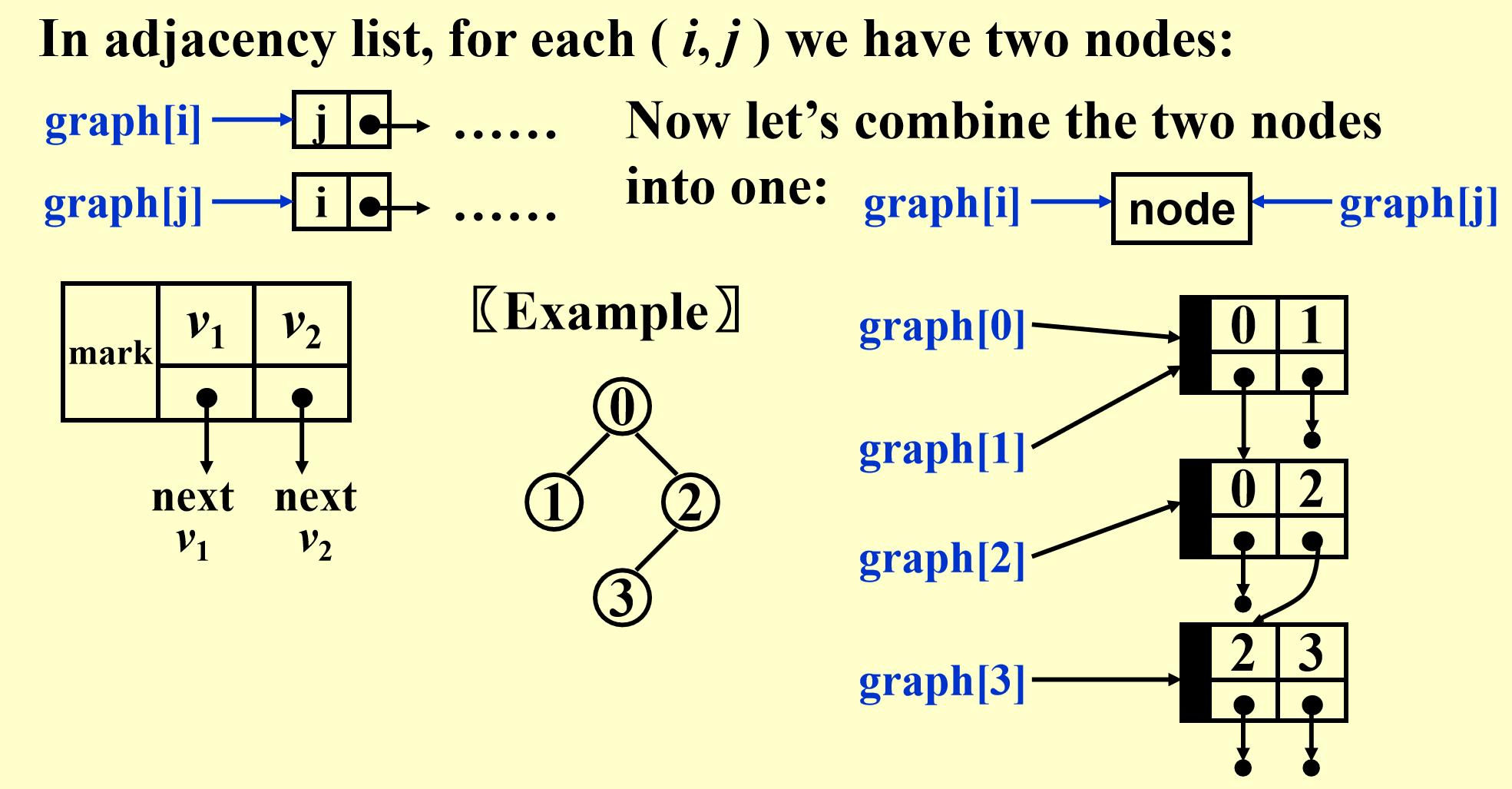
image-20231113151045130

Weighted Edges

  • 数组：直接把值变成weight
  • adjacency lists / multi-lists: add a weight field to the node

Topological Sort 拓扑排序

AOV Network

事件发生在边上，只要到达顶点，事件就结束了

V(G): activities

E(G): 优先级关系

image-20231113152049226

Partial order：传递性、非自反性（项目必须可行）

可行的AOV网络必须是DAG(有向无环图)

topological order

拓扑顺序是图中顶点的线性排序，对于任意两个顶点\(i, j\)，如果\(i\)是网络中\(j\)的前导，则\(i\)在线性排序中先于\(j\)

  • 解决的是次序问题，不是排序问题

  • 拓扑排序的结果是不唯一的

  • in-degree为0的节点是拓扑排序的起点

void Topsort( Graph G )
{   
    int  Counter;
    Vertex  V, W;
    for ( Counter = 0; Counter < NumVertex; Counter ++ ) 
    {
        V = FindNewVertexOfDegreeZero( ); /*O(|V|) V的模长 - 集合V中的个数*/
        if ( V == NotAVertex ) 
        {
            /*同时解决了判断图里有无环路的问题*/
            Error ( “Graph has a cycle” );   
            break;  
        }
        TopNum[ V ] = Counter; /* or output V */
        for ( each W adjacent to V )    Indegree[ W ] – – ; /*解除依赖关系，时间复杂度是边的个数*/
    }
}

\(T=O(|V|^2+|E|)=O(|V|^2)\) 利用边和顶点的关系化简

优化算法：（常考项！！）

void Topsort( Graph G )
{   
    Queue  Q;
    int  Counter = 0;
    Vertex  V, W;
    Q = CreateQueue( NumVertex );  
    MakeEmpty( Q );
    for ( each vertex V )   
        if ( Indegree[ V ] == 0 )   Enqueue( V, Q );

    while ( !IsEmpty( Q ) ) 
    {
        V = Dequeue( Q );
        TopNum[ V ] = ++ Counter; /* assign next */
        for ( each W adjacent to V )
            if ( – – Indegree[ W ] == 0 )   Enqueue( W, Q );
    }  /* end-while */
    if ( Counter != NumVertex ) Error( “Graph has a cycle” );
    DisposeQueue( Q ); /* free memory */
}

\(T = O(|V| + |E|)\)

最短路算法

  • 输入：

    • 有向图\(G=(V,E)\)
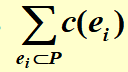
    • cost function (weight) \(c(e)\) for \(e\) in \(E(G)\) \(/rightarrow\) length = image-20231120142427477

  • 计算点到点的最短路和遍历点计算全局最短距离的复杂度是一致的

  • 限制条件：如果有negative的weight并且形成了Negative-cost cycle，最短路无解

    • 如果不存在Negative-cost cycle，则定义从s到s的最短路径为零

Unweighted Shortest Paths - 不带权重的最短路

  • 等价于Breadth-first-search

  • 实现方式（图论都会有一个table结构）： 

    Table[ i ].Dist ::= distance from s to vi  /* initialized to be ∞ except for s */
Table[ i ].Known ::= 1 if vi is checked; or 0 if not
Table[ i ].Path ::= for tracking the path   /* initialized to be 0, 记录cost来源 */

  • 算法1 
    void Unweighted( Table T )
{
    int  CurrDist;
    Vertex  V, W;
    for ( CurrDist = 0; CurrDist < NumVertex; CurrDist ++ )
    {
        for ( each vertex V )
      if ( !T[ V ].Known && T[ V ].Dist == CurrDist ) 
            {
          T[ V ].Known = true;
          for ( each W adjacent to V )
              if ( T[ W ].Dist == Infinity )
                    {
            T[ W ].Dist = CurrDist + 1;
            T[ W ].Path = V;
              } /* end-if Dist == Infinity */
      } /* end-if !Known && Dist == CurrDist */
    }  /* end-for CurrDist */
}
    \(T=O(|V|^2)\)，e的个数的复杂度被它的bound省掉了
    Distance和Known造成了冗余
  • 算法2 - 使用queue优化 
    void Unweighted( Table T )
{   
    /* T is initialized with the source vertex S given */
    Queue  Q;
    Vertex  V, W;
    Q = CreateQueue (NumVertex );  
    MakeEmpty( Q );
    Enqueue( S, Q ); /* Enqueue the source vertex */
    while ( !IsEmpty( Q ) ) 
    {
        V = Dequeue( Q );
        T[ V ].Known = true; /* not really necessary */
        for ( each W adjacent to V )
            if ( T[ W ].Dist == Infinity ) 
            {
                T[ W ].Dist = T[ V ].Dist + 1;
                T[ W ].Path = V;
                Enqueue( W, Q );
            } /* end-if Dist == Infinity */
    } /* end-while */
    DisposeQueue( Q ); /* free memory */
}
    \(T=O(|V|+|E|)\)

Dijkstra's Algorithm (for weighted shortest paths) - 带权重的最短路

！！重点 ！！

  • 前提条件：不带负边
  • 定义一个\(S\) - { s and vi’s whose shortest paths have been found }（由起始点和已知最短路的点构成）
  • 思路：贪心算法，cost随着加edge的过程是递增的，因此当前最小就是全局最小

  • image-20231120150943829 

      void Dijkstra( Table T )
  {   
      /* T is initialized by Figure 9.30 on p.303 */
      Vertex  V, W;
      for ( ; ; )
      {
          V = smallest unknown distance vertex;
          if ( V == NotAVertex )
            break; 
          T[ V ].Known = true;
          for ( each W adjacent to V )
            if ( !T[ W ].Known ) 
                if ( T[ V ].Dist + Cvw < T[ W ].Dist )
                  {
                    Decrease( T[ W ].Dist  to
                            T[ V ].Dist + Cvw );
                    T[ W ].Path = V;
                } /* end-if update W */
      } /* end-for( ; ; ) */
  }

  • 对于V = smallest unknown distance vertex的不同实现方式：

    • Implementation1 - scan image-20231120152539099
    • Implementation2 - heap image-20231120152601828
      • Method1
        • 第一项：每个顶点处理一次然后deletemin - find the smallest unknown
        • 第二项：Decrease
      • Method2 直接insert，不进行decrease

有负边(no negative cycle)的情况

void  WeightedNegative( Table T )
{   
    /* T is initialized by Figure 9.30 on p.303 */
    Queue  Q;
    Vertex  V, W;
    Q = CreateQueue (NumVertex );  
    MakeEmpty( Q );
    Enqueue( S, Q ); /* Enqueue the source vertex */
    while ( !IsEmpty( Q ) )
    {
        /* each vertex can dequeue at most |V| times */
        V = Dequeue( Q );
        for ( each W adjacent to V )
            if ( T[ V ].Dist + Cvw < T[ W ].Dist ) 
            {
                /* no longer once per edge */
                T[ W ].Dist = T[ V ].Dist + Cvw;
                T[ W ].Path = V;
                if ( W is not already in Q )
                    Enqueue( W, Q );
            } /* end-if update */
    } /* end-while */
    DisposeQueue( Q ); /* free memory */
}

\(T=O(|V|×|E|)\)，没有known set了

DAG - 有向前趋图

顶点可以按拓扑顺序选择，因为当一个顶点被选择时，如果没有任何来自未知节点的边，它的距离就不能再降低。

\(T = O( |E| + |V| )\) and no priority queue is needed.

  • AOE (Activity On Edge) Networks的应用 - CPM

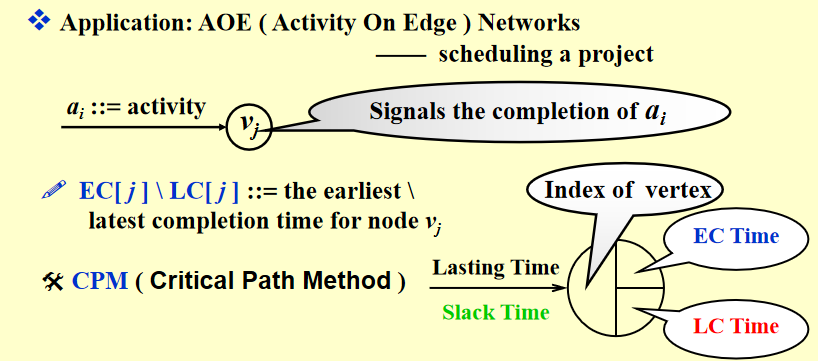
    • image-20231120154130606

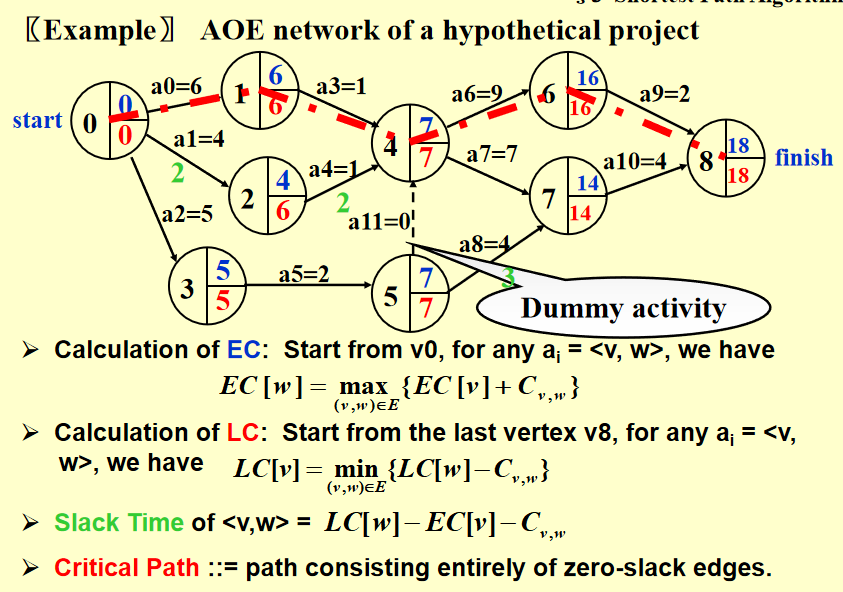
    • e.g. image-20231120154440767

所有顶点最短路 - 直接遍历所有顶点解最短路图

image-20231120155138378

最大流问题

方法1：最开始的残差图是原来的图，不断寻找最短路（从流量最少的开始）存入flow graph并在残差图中删除，直到残差图中没有最短路：

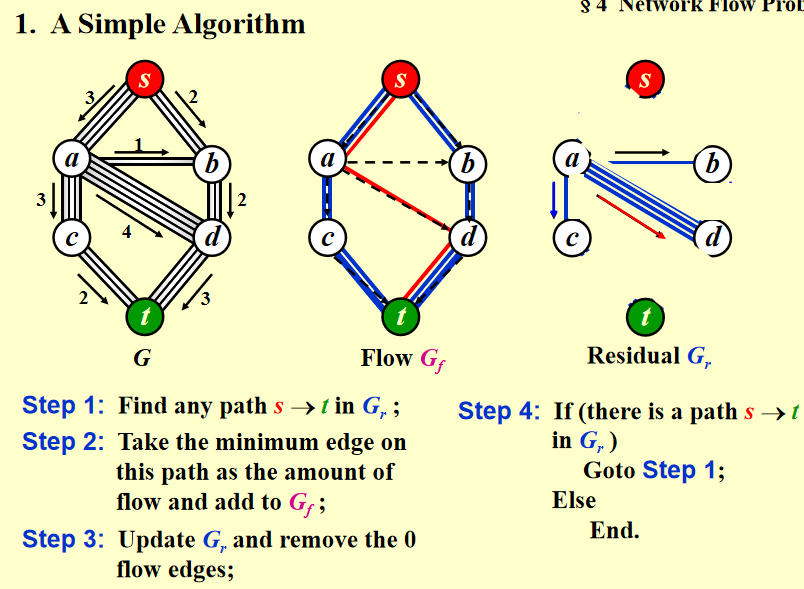
image-20231127143733384

方法2：每次对于被选中的边，在残差图中add一个反向的边，这个算法可以得到全局最优解

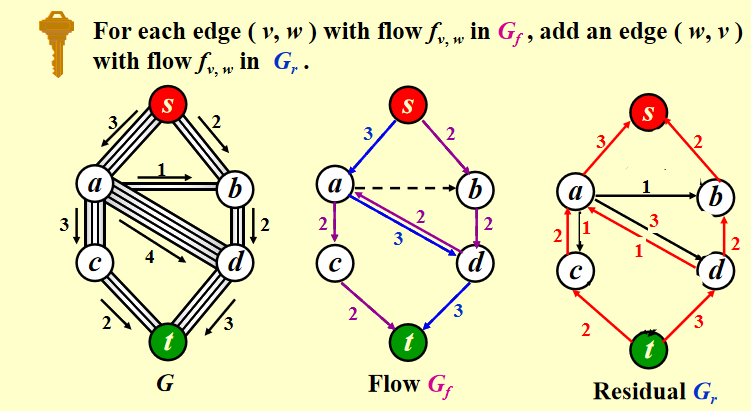
image-20231127144258501

具体实现1： 把G看成无权图，每次使用bfs找到一条路径然后对残差图添加反向路径，直到没有路径可找

\(T=O(f·|E|)\) where \(f\) is the maximum flow.

具体实现2： 类Dijkstra's algorithm，只不过每次选known vertex的标准是allows the largest increase in flow

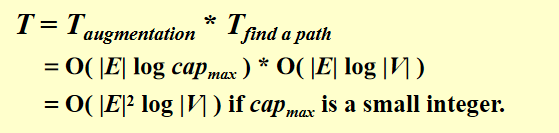
image-20231127150549470

具体实现3：在具体实现1的基础上减去的路径数不是1而是整个路径的流量的最小值

image-20231127210842215

note：

  • 如果每一个不属于{s,t}的角都只有一个入边或一个出边，那么时间的bound会被减少到\(O(|E||V|^{1/2})\)
  • 最小成本流问题是在所有最大流量中，在每条边都有单位流量成本的情况下，找出一个成本最小的流量

最小生成树

图G的生成树是由V(G)和E(G)的子集组成的树

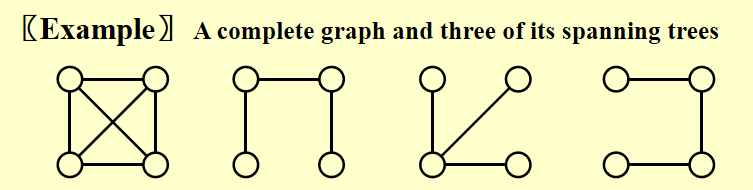
image-20231127145830260

  • 最小生成树是树，因为它是无环的——边的个数是|V| - 1

  • 它是最小的，因为边的总成本是最小的

  • 它是生成的，因为它覆盖了每个顶点

  • 如果G连通，则存在最小生成树

  • 在生成树中加入一条非树边，得到一个环

算法1 贪心算法

  • 我们必须只使用图中的边
  • 必须精确地使用|V|-1条边
  • 我们不会使用产生cycle的边

使用类似Dijkstra's algorithm遍历点，使用并查集判断是否有cycle

  • 此处并查集也可以用loop简化判断，但是Kruskal's Algorithm不可以

算法2 Kruskal’s Algorithm——maintain a forest

建堆，把所有边都放在堆里面

void Kruskal ( Graph G )
{   
    T = { };
    while  ( T contains less than |V| - 1 edges && E is not empty ) 
    {
        choose a least cost edge (v, w) from E;
        delete (v, w) from E;
        if  ( (v, w) does not create a cycle in T ) add (v, w) to T;
        else    discard (v, w) ;
    }
    if  ( T contains fewer than |V| - 1 edges )
        Error ( “No spanning tree” ) ;
}

\(T=O(|E|log|E|)\) 遍历每条边*deletemin

DFS的应用

先序遍历的普遍形式

void DFS ( Vertex V )  /* this is only a template */
{   
    visited[ V ] = true;  /* mark this vertex to avoid cycles */
    for ( each W adjacent to V )
        if ( !visited[ W ] )
    DFS( W );
} /* T = O( |E| + |V| ) as long as adjacency lists are used */

1. 无向图

void ListComponents ( Graph G ) 
{   
    for ( each V in G ) 
        if ( !visited[ V ] ) 
        {
    DFS( V );
            printf(“\n“);
        }
}

2. Biconnectivity - 双向连通性

  • v是articulation point如果去掉v会使得图被分为（至少）两个连通分量

  • G是biconnected graph如果：

    • G是connected
    • 没有articulation point

  • 双向连通分量 - 最大双向连通子图

    • 单个节点是一个双向连通分量
    • 两个或多个双连接分量不能共享任何边。因此E(G)被G的双连通分量分割。

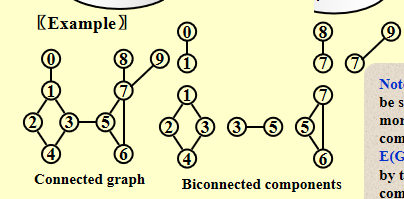
image-20231204204350375

寻找双连通分量

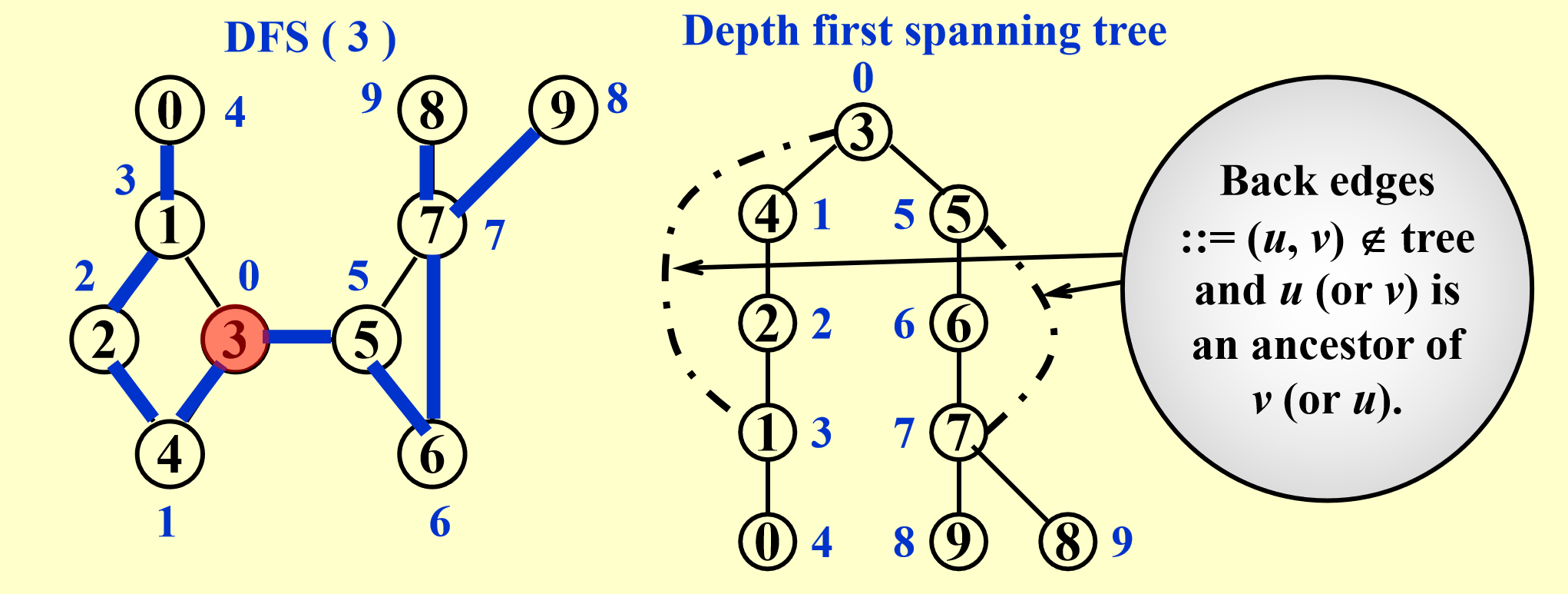
image-20231204205243176

  • DFS获得生成树，记录DFS访问顺序 - If u is an ancestor of v, then Num( u ) < Num( v )
  • 把原图中没有出现在spanning tree的边用虚线表示
  • 寻找articulation point：
    • 如果根结点至少有2个子结点，那么它就是一个articulation point
    • 其他节点articulation point是当且仅当：
      • 有至少一个child
      • 不可能向下走至少一步之后可以跳到u's ancestor - 例如这张图依据这个性质排除了2、4、6

具体算法： - 定义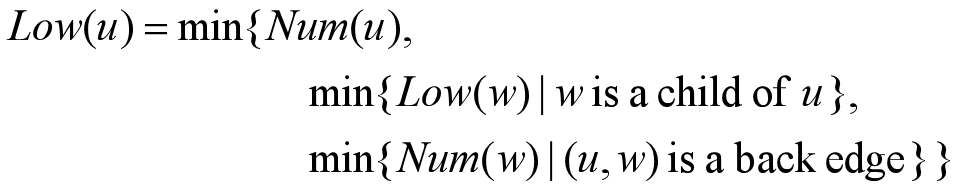：image-20231204210231459 - 根节点和不含back edge的叶节点的Low number就是自己的num

  • articulation point条件：
    • 至少有两个孩子的根节点
    • 至少有一个孩子且Low(child) >= Num(u)的其他节点

3. 欧拉环

定义：一笔画且在起始点结束（不考虑起始点的是欧拉路径）

  • 只有当图是连通的并且每个点是偶数度时，欧拉环才可能存在
  • 如果恰好有两个奇数度的顶点，欧拉路径是可能的，并且必须从其中一个奇数度顶点开始

输出欧拉环：多轮DFS（算法目的：寻找一张图有几个欧拉环）

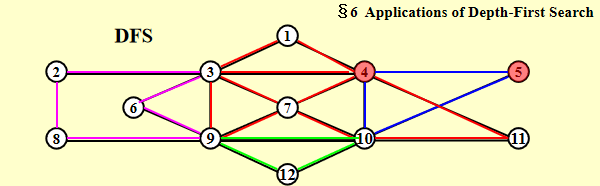
image-20231204213000721

  • 该路径应该被维护为一个链表

  • 对于每个邻接表，维护一个指向最后扫描到的边的指针

  • \(T=O(|E|+|V|)\)

Find a simple cycle in an undirected graph that visits every vertex – Hamilton cycle