跳转至

数字逻辑设计期末复习

时序电路部分：时序电路整理

chapter1

进制转换

  • 整数的转换

    • Binary - 二进制
    • Octal - 八进制
    • Decimal - 十进制
    • Hexadecimal - 十六进制
    • 一般在其他进制转换的过程中都是以二进制为桥梁的

  • 小数的转换

    • DtoB - 乘2进1法
    • BtoOther - 从小数点开始从左到右取n位转换
    • 由于小数部分不存在“最小精度”的说法，所以有可能十进制无法精准转化为二进制，但是二进制可以转化为十进制

二进制与编码的转换

  • BCD码 - 4位二进制表示1位十进制
    • 运算过程中的进位（补6）问题 - 8 + 5 = 1000 + 0101 = 1101 补6 1101 + 0110 = 1 0011，其中1作为carry
    • Excess3（余3码）- 在 BCD码的基础上，增加一个大小为 3 的偏移量
      • 方便判断进位，不过运算后还得修正：如果结果没进位，则减去 3；如果结果进位了，则加上 3
  • one-hot/one-cold

  • ASCII码 - 字符编码 image-20240103113642500

  • Parity Bit - 奇偶校验位

    • 看清奇偶 - 加上校验位后1的个数
    • 看清最高位校验还是最低位校验

  • Gray Code - 格雷码，相邻两个数在二进制表示下只差一位

    • 寻找第k个格雷码：\(k\) XOR \((k>>1)\)
    • “镜像技巧”：image-20240103121346864

chapter2

布尔代数

  • 达摩根律 - break the line, change the sign
  • 分配律
    • \(X + YZ = (X+Y)(X+Z)\)
  • 一致性定理
    • \(XY+\bar{X}Z+YZ=XY+\bar{X}Z\)
    • \((X + Y)(\bar{X} + Z)(Y+Z)=(X+Y)(\bar{X}+Z)\)
  • the dual - 对偶性质
    • 翻转0/1和AND/OR
    • 不翻转布尔变量
    • 不改变原先优先级顺序
    • 等式两边对偶后仍然成立

Complement of a function 互补函数

  • OR \(\leftrightarrow\)AND
  • 0's \(\leftrightarrow\)1's
  • \(X\leftrightarrow\bar{X}\)
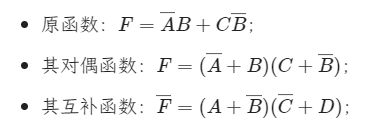
  • 一个 函数的互补(Complement of a Function) 指的是，将它的 对偶函数 中每一个 变量 都取反得到的函数，而该函数正好等于原函数的 非：image-20240103123218405
  • 也可以直接取非之后使用达摩根律

Canonical form（规范形式）

  • 最小项之和(Sum of Minterms, SOM)
    • “枚举所有1的可能”
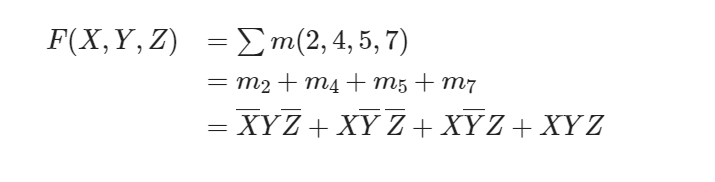
    • image-20240103125320192
  • 最大项之积(Product of Maxterms, POM)
    • “枚举所有0的可能”
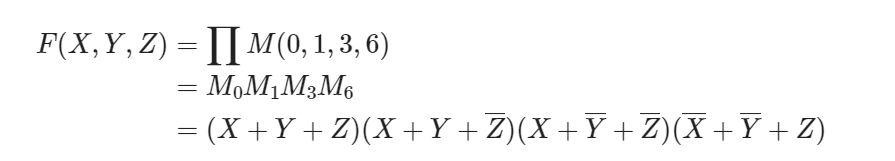
    • image-20240103125515725
  • index 最小项直接转换二进制，最大项则取反转换二进制
    • 相同index的最小项和最大项是取反关系

Standard form（标准形式）

  • SOP(Sum of Products) - SOM的化简形式
  • POS(Product of Sums) - POM的化简形式

  • 混合表达（大于两层电路）不是标准形式

  • 把标准形式expand成规范形式：

    • 最小项：补充 \(1 = X + \bar X\)
    • 最大项
      • 先变成积（使用分配律）
      • 补\(X·\bar X\) 再使用分配律
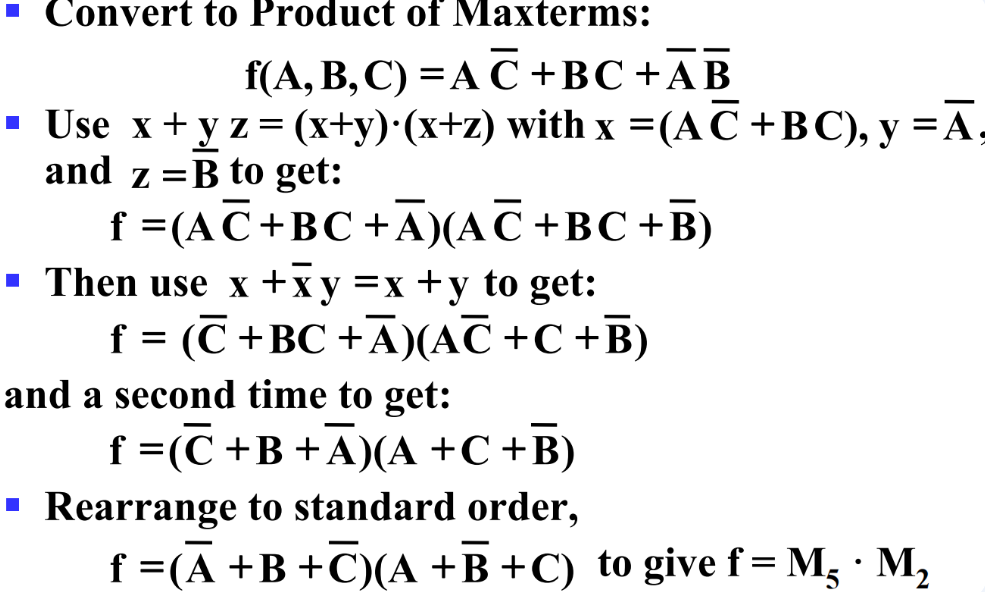
      • image-20240728184017123
    • 其实我觉得真值表更方便

门输入代价

  • Literal Cost 文字代价

    • \(L\)：表达式中Literal个数
    • 相等的\(L\)下电路复杂度不一定一样
    • 第一层次的输入引脚数

  • Gate Input Cost 门电路输入代价

    • \(G\)：点完文字代价的基础上（一层结合之后（？）对文字的组合再次清点（remaining OR gate inputs）
      • 最后那个大项不用点
    • \(GN\)：点完门电路输入代价的基础上考虑非门输入个数
      • 注意去除可以共享的非门，两个\(\bar B\)算+1个\(GN\)

卡诺图优化

  • 格雷码排布
  • 尽可能大圈
  • 避免冗余优化
  • 合理使用don't cares
  • 是规范形式和标准形式的桥梁
  • Implicant - 蕴涵项
    • a product in SOP or a sum in POS
    • in K-map - a group containing \(2^n\) squares
    • 两类蕴涵项：
      • prime implicant - 主蕴涵项
      • 极大蕴涵项
    • essential prime implicant - 基本主蕴涵项
      • 包含 只被它(基本主蕴含项)覆盖的 1 的主蕴含项

逻辑门

  • NAND/NOR - universal gate 通用门

  • XOR - 异或/XNOR - 同或

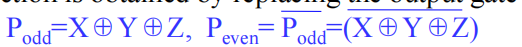
    • 多输入的异或/同或称为奇/偶函数image-20240106184540972

    • 奇偶校验：

      • 使用奇函数（异或）生成偶校验位
      • 使用偶函数（同或）生成奇校验位
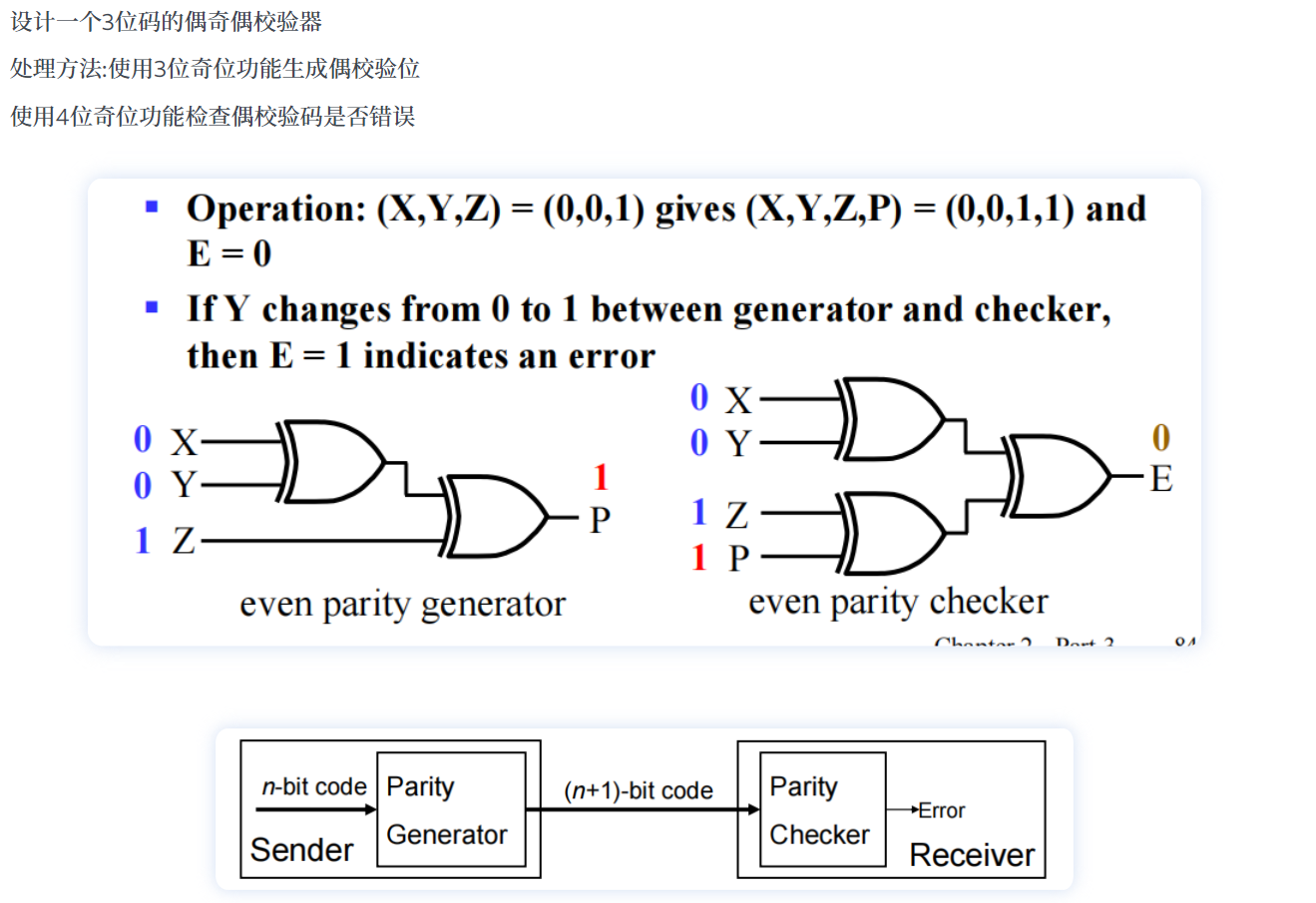
      • image-20240103155116933

  • Buffer - 缓冲器

  • 3-state buffer - 三态门
    • 使用使能信号选择输出接收哪个输入，具体到一个门就是是否接收该输入
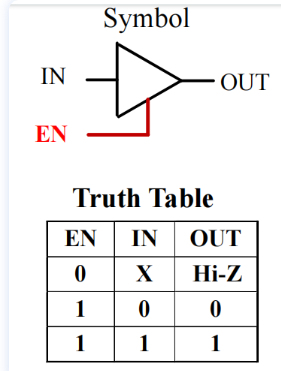
    • image-20240103154836641

exercise1: \(F=(\bar{D+C·\bar{AB}})·(\bar{\bar{AB}·\bar{C+D}})=\bar{D}·(\bar{C}+AB)·(AB+C+D)=AB\bar{D}\)

Chapter3&5

工艺参数

fan-in - 一个逻辑门可用的输入数量

fan-out - 一个逻辑门输出时可驱动的标准负载数量

  • 一般负载数量增加转换时间也会增加，而最大负载就是由最大转换时间下的负载数量决定的

noise margin - 对外界噪声的容忍能力(具体来说是不会导致行为异变的最大噪声阈值)

cost - 门对集成电路成本的贡献的度量 - Gate cost

transition time - 转换时间

  • \(t_{LH}\) - rise time
  • \(t_{HL}\) - fall time
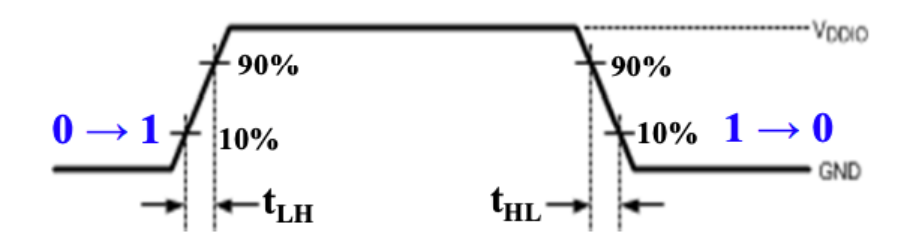
  • image-20240106194257302

propagation delay - 传播延迟

  • 注意判断hl还是lh是看传播到输出的变化
  • \(t_{PHL}\) - propagation delay high-low
  • \(t_{PLH}\) - propagation delay low-high

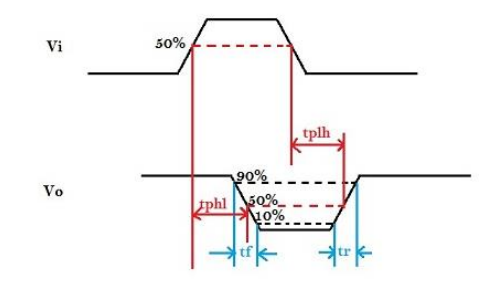
  • image-20240106194611428

  • \(t_{pd}\) - 统一表示传播延迟时间，是hl和lh的average或者max

power dissipation - 电源输出能耗和门的能耗

inertial delay - 引入了 拒绝时间(rejection time)，只有当输入达到一定能量后，才会出发栅极输出（在这种模型下，噪音等会被过滤）

  • image-20240106195631665

calculate gate delay based on fan-out:

  • \(t_{pd}\) = 固定延迟 + SL（标准化负载量） * 一个标准负载带来的延迟系数

逻辑设计

表示逻辑的方法：

  • Truth Table - 真值表
  • Timing Diagram - 时序图
  • Boolean Function - 布尔函数
  • Karnaugh Maps - 卡诺图
  • Logic Circuit - 逻辑电路图

斜体表示 表达方式不唯一

设计过程：specification - 确定系统的行为\(\rightarrow\)formulation - 逻辑表达\(\rightarrow\)optimization - 优化\(\rightarrow\)technology mapping - 工艺映射\(\rightarrow\)verification - 正确性验证

Hierarchical Design - 分层设计

  • Top-Down 自顶向下 - 从需求开始，自顶向下分解功能设计
  • Bottom-up 自底向上 - 根据现有的元件去组合成目标功能

工艺映射步骤

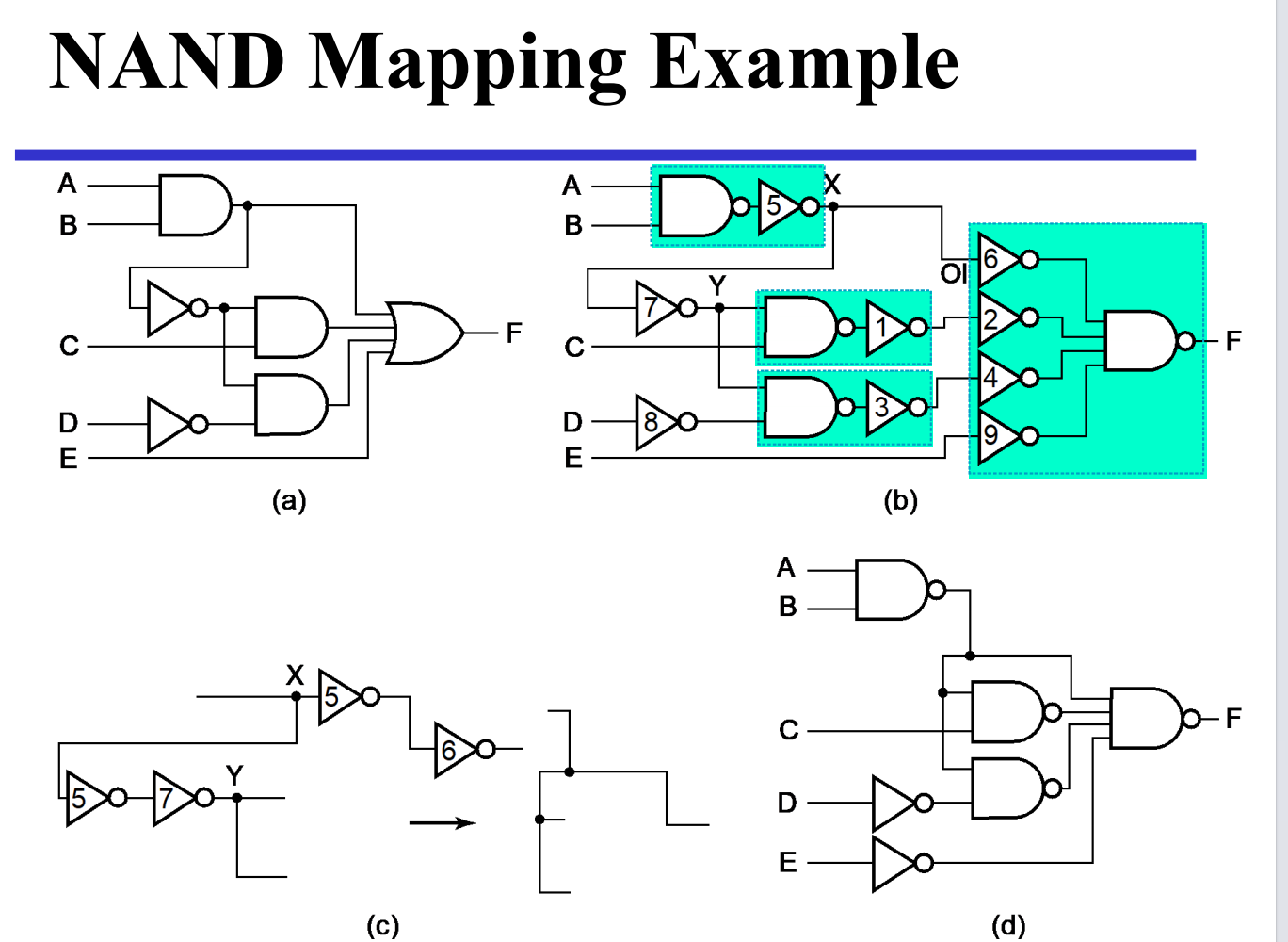
49945506dadee6c9163ac7b9a77fc65

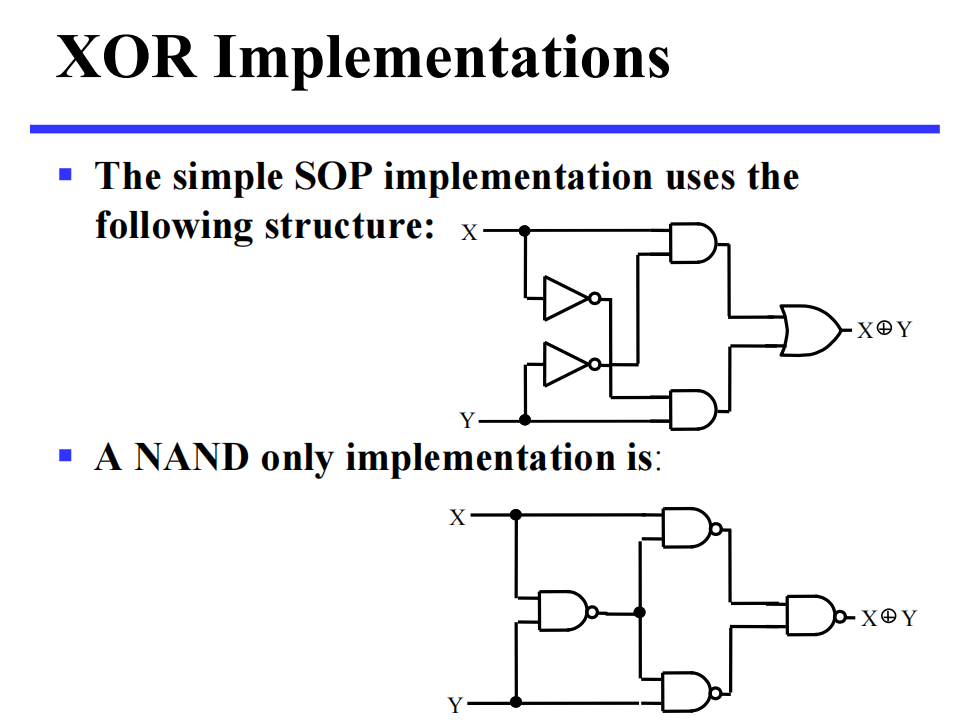
9b0dbab0607e710d1b68d3a473def64

组合功能模块

Decoder - 译码器

  • n inputs and m outputs with n ≤ m ≤ \(2^n\)

  • 本质上是枚举最小项

  • 输出太多时，考虑fan-out的限制，我们采取分层设计：

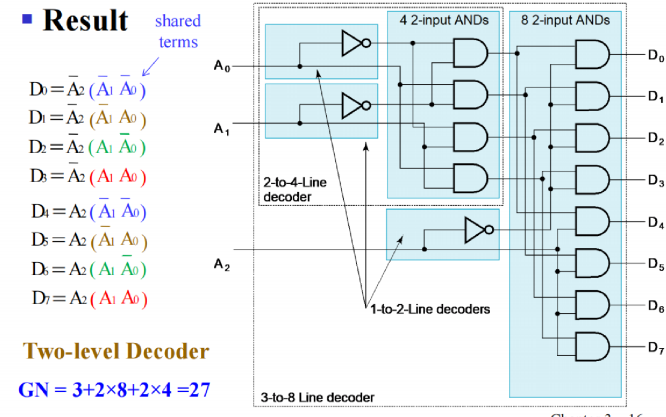
image-20240106205710031

Encoder - 编码器

  • m inputs and n outputs with n ≤ m ≤ \(2^n\)

  • 普通编码器必须要求输入是 one-hot 的，即只允许存在一个输入为 1，否则无法判断得出唯一输出。

  • 优先编码器（Priority Encoder）能够实现优先级函数，它不要求输入是 one-hot 的，而是总是关注有效输入中优先级最高的那一个。即比如当优先级最高的那一位是 1 时，其它所有优先级不如它的位置的值都是我们不关心的内容了。

Multiplexer - 多路选择器

  • n control inputs (selection inputs), m inputs and one output with m < \(2^n\)
  • 通常，一个\(2^n-to-1\)MUX的组成为：
    • 一个\(n-to-2^n\)译码器（MUX 利用了译码器每次只有一个输出为 1 的特性，从而实现选择功能）
    • \(2^n*2\) AND-OR / 利用三态门代替AND-OR门（减少门输入）
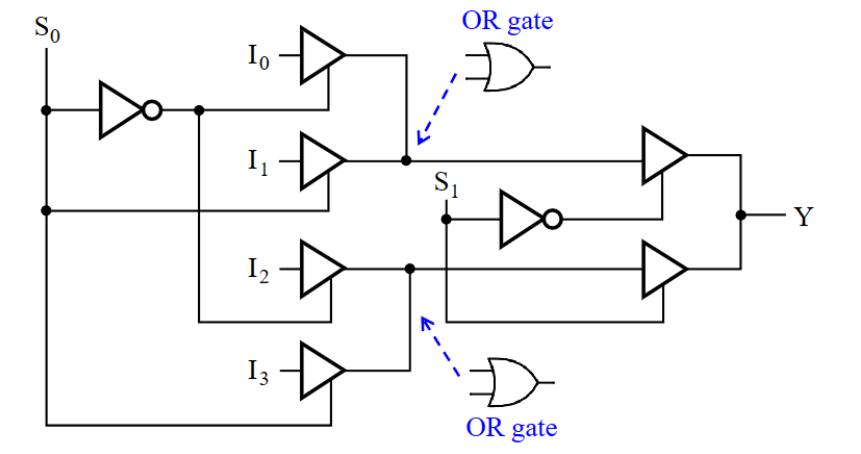
      • 完全使用三态门实现4to1MUX: image-20240106231810418
    • MUX的本质是函数的实现

Programmable implementation technologies - 可编程技术

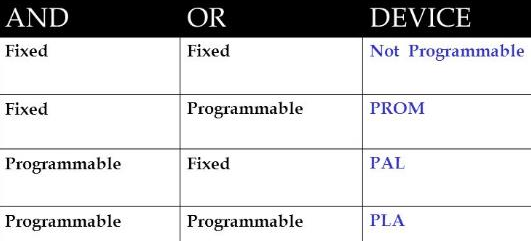
image-20240107133217156

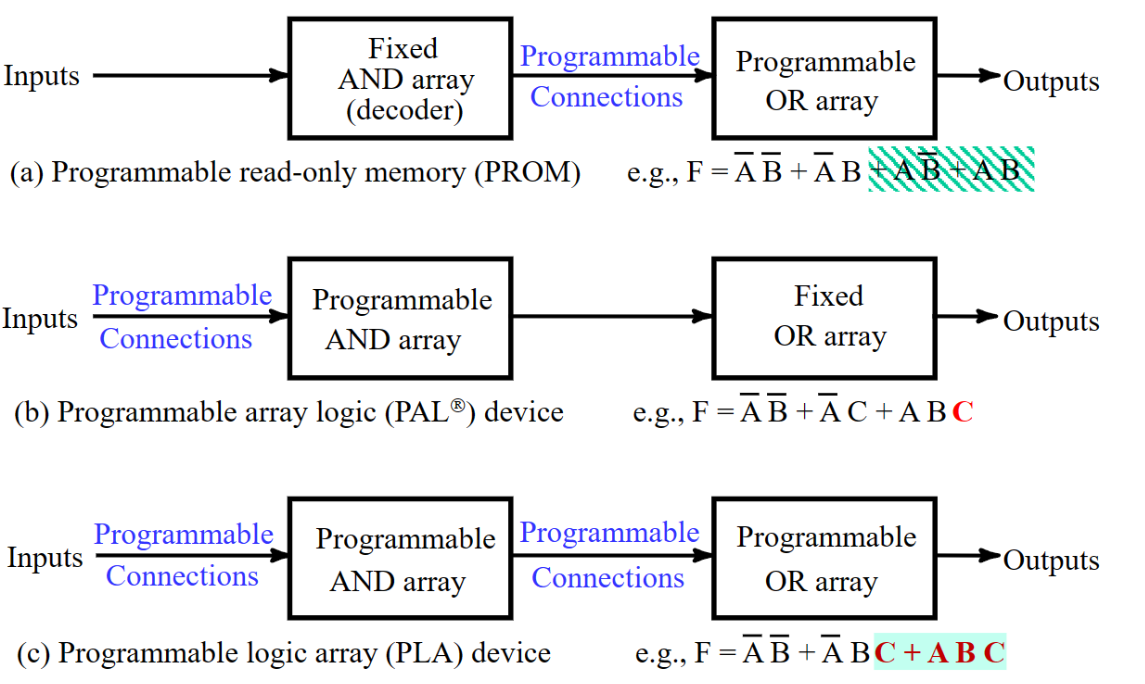
image-20240107134655785

  • PROM/ROM - read only memory
    • 不改变项的内容，只缩短相加的项数
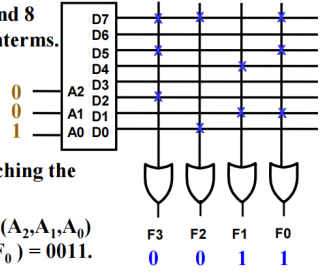
    • image-20240107133318275
  • PAL - Programmable Array Logic Devices
    • 不改变项数，可以改变项的内容
    • 有⼀组可编程的ANDs和固定的ORs（OR的数量是固定的）相结合，⼀旦超过3个项的与或者或，就要利⽤中间变量进⾏迭代
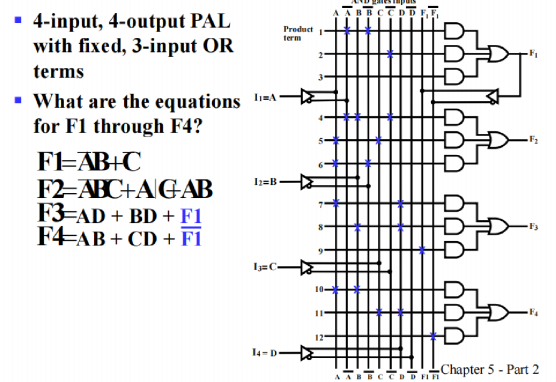
    • image-20240107133720949
  • PLA - Programmable Logic Array
    • 项数可以改变，也可以改变项的内容
    • 前端对变量扩展、重编程，有⼀组可编程的ANDs和⼀组可编程的ORs
    • 输出端不⽌⼀次重编程，输出前的异或相当于直接输或者取反，取反可以达到增加输⼊项的⽬的 - 因此我们在设计的时候可以画卡诺图观察互补性
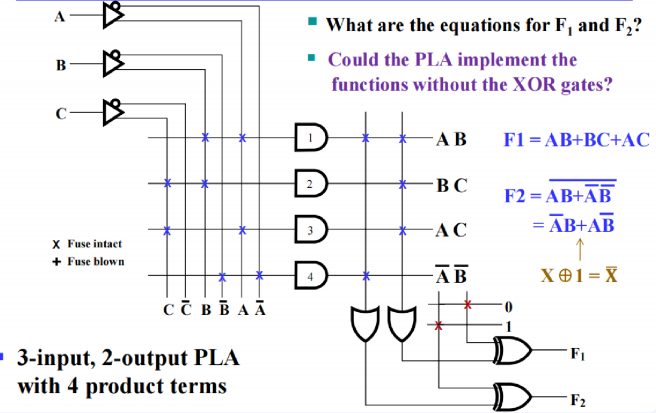
    • image-20240107134124653
  • Lookup Table - 查找表
    • 通过让数据源接内存，并通过修改真值表内的值，即修改内存里的值，来实现数据源的变化，来改变 MUX 的行为。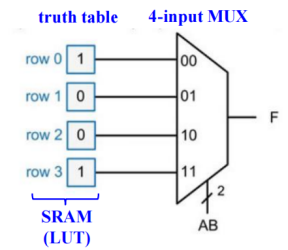
    • image-20240107135320179
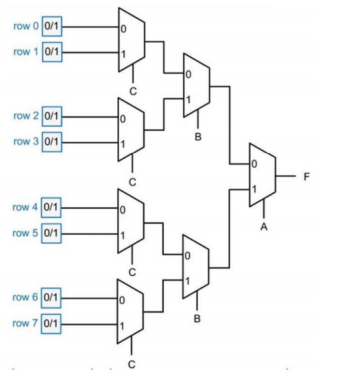
    • 而在实际工艺过程中，会利用a tree of smaller MUXes 组 成 ⼀ 个 ⼤ MUX：image-20240107135403177
  • FPGA
    • 复习ppt上面没有提到这个考点，所以我就粗略整理了
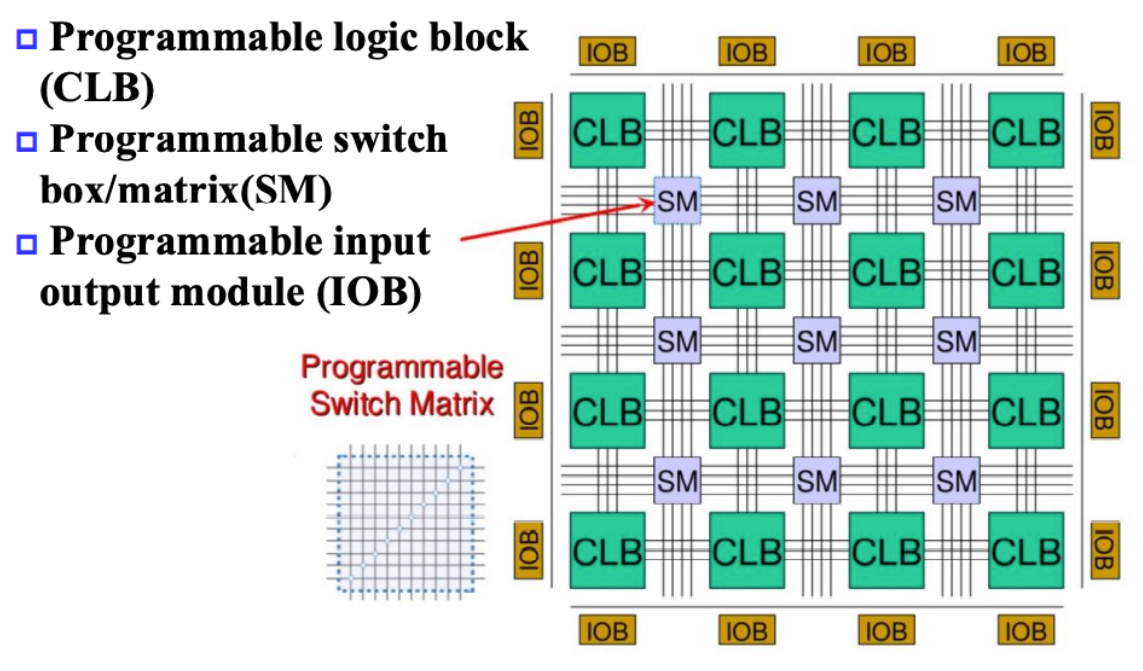
    • image-20240107135604377
    • CLB(Configurable Logic Block)
      • 大量存储 LUT
    • SM(Switch Matrix)
      • 可编程的交换矩阵
    • IOB(Input & Output Block)
      • 可编程的输入输出单元

加法器

Half Adder - 半加器

  • \(S=X\bigoplus Y\)
  • \(C=XY\)

Full Adder - 全加器

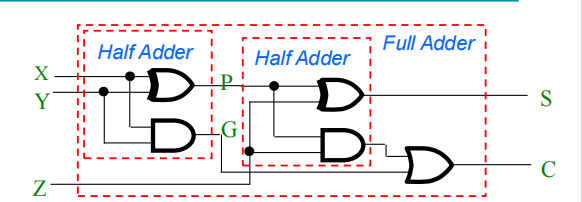
image-20240107000752474

  • \(S=X\bigoplus Y\bigoplus Z\)

  • \(C=XY+(X\bigoplus Y)Z\)

    • carry generate - \(XY\)，进位产生项
    • carry propagate - \(X\bigoplus Y\)，进位传播项

  • 半加器和全加器的区别就是2/3输入的区别，半加器不接收之前的进位信息

Binary Ripple Carry Adder - 行波进位加法器

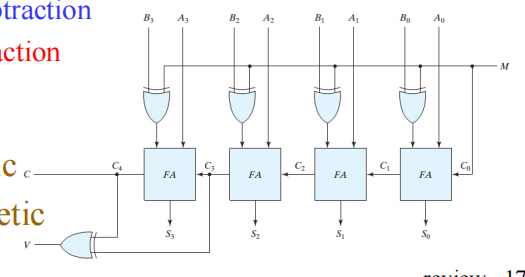
image-20240107002647628

  • 全加器实现的行波进位加法器的复杂度比较高，进位的传递非常漫长

Carry Lookahead Adder (CLA) - 超前进位加法器

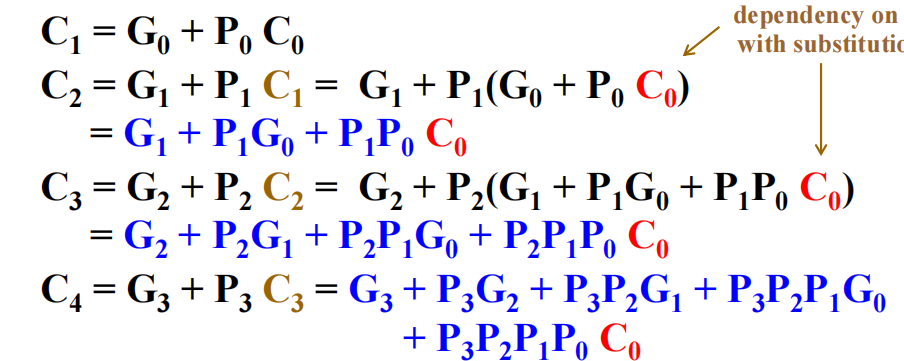
  • 使用GP的划分，因为GP的值都只与当下的两个XY输入相关，因此我们对进位传递的优化只需要考虑上一个进位的提前计算，也就是迭代解决这个问题：image-20231108115305020
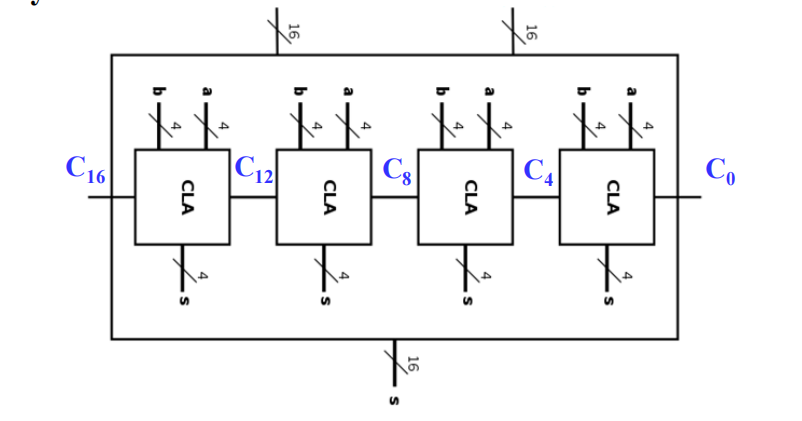
  • 又因为在工艺映射的过程中fan-in的限制，我们采取Group Carry Lookahead Adder - 模块化超前进位加法器的方式，组内提前进位，组间行波进位：image-20231108120456826

二进制计算

补码计算：从低位到高位扫描

  • 复制所有最低有效的0
  • 复制第一个出现的1
  • 接下来所有位取反

对有符号数，反码和补码的计算是保留符号位（最高位）的，也就是说最高位始终为1（表示负权重）。

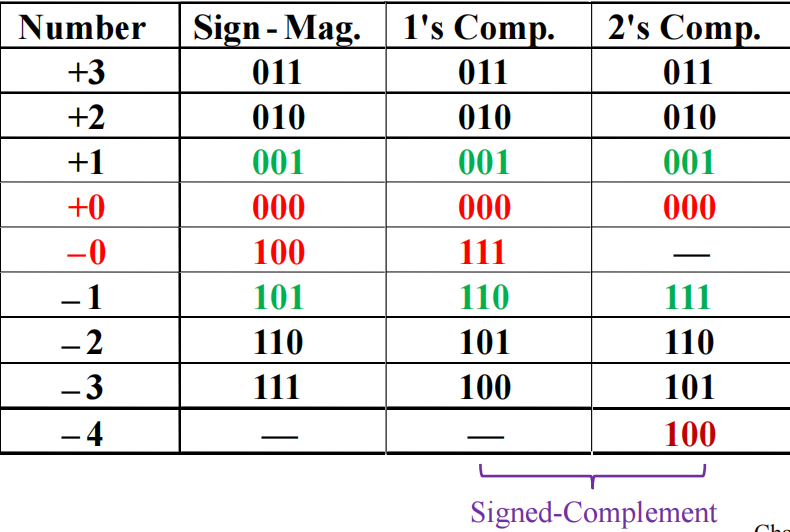
image-20240107125702015

符号拓展：将符号位复制到更高位。

无符号二进制减法：先加上被减数的补码，如果得到的进位是1，则不用修改；否则取结果的补码并加上负号作为最终的答案。

带符号的二进制数运算：先将所有数变成带符号的二进制补码进行运算，再舍弃溢出位、转换回来。运算时减法取减数的无符号二进制补码（我的理解是化减为加）进行计算。

image-20240107124851767